Decoding Strategies for Text Generation

Finding the humanity in approximating a NP-Hard problem

Introduction

Recently, machine learning models have seen incredible progress towards computers being able to generate text that sounds human. This is an area of research that involves both furthering our understanding of machine intelligence as well as language use in society. I think it’s an interesting problem because it once against prompts a long-standing question in machine intelligence: what does it mean to be human?

So how do we make computers sound human? We'll explore this in two ways. The first is understanding why this problem is so computationally challenging and the second is to outline the different approaches we can take using a special kind of machine learning model known as a language model. In its simplest sense, a language model assigns a probability to a sequence of words. As you can imagine, language is infinite and so we can’t possibly know the probability of the phrase “cat in the hat”. However, our machine learning model (by definition) is going to approximate this likelihood for us. And, as it turns out, this is a powerful technique that works incredibly well for practical purposes of generating human-sounding text.

In this blog post, I want to motivate why this task of generating text is computationally difficult, and even if we had the "optimal solution", why it may not fit our idea of what good text sounds like. Afterward, we'll walk through a few modern approaches to remedy this. As we'll see, these approaches work really well.

Our Objective

We can use the chain rule in probability to break down a sequence (or sentence) of words into step-by-step calculations. Let's say we are looking for the probability of the phrase "cat in the hat":

We can break this value down into the product of the following terms (where $\text{<s>}$ denotes the starting token):

But how do we get these probabilities to start? That's what the language model is for. In essence, a language model’s purpose is to give us $P(w ~|~ c)$, where $w$ is a particular target word (i.e. the next word) and $c$ is the context that precedes the target word. Using a trained model, we can use $P(w ~|~ c)$ to create a distribution of the likelihood for the next word.

Now, we turn our focus to using these probabilities to create text. Let's determine what the first word of our generation would be. Similar to the previous example, where we have a $\text{<s>}$ token to signify the beginning of a sequence, we can ask the model what the value of $P(w ~|~ \text{<s>})$ for a variety of different values of $w$. But how do we select what $w$ should be when we're given the probabilities for every possible word? Is it simply the highest value?

More broadly, our goal is to select the words that maximize:

But how do we do this using the model's outputted probabilities? As we will see, this is the million dollar question - literally.

Showing NP-Hardness

Before moving on to approaching a solution, it’s worth gaining a little appreciation for how difficult this problem truly is. To solve it in its entirety, you would make a million dollars! Literally!

The challenges we have with using our machine model to generate text is yet another manifestation of the NP-Complete class of problems (in it’s decision form). If you are unfamiliar, these problems are known to be the toughest problems in computer science. What’s more interesting, is that problems existing in this class can all be reduced to one another, implying that they are all in essence the same problem.

Wait it's all 3-SAT? (Always has been.)

Let’s show that our issue of finding the most likely sequence is just as hard as the other famous NP-hard problems, like the Traveling Salesman Problem and Knapsack Problem.

Generating text is akin to the problem of finding the highest probability sequence that starts with $\text{<s>}$. The easiest reduction to see is if we construct a directed graph, starting with $\text{<s>}$, and layers consisting of each word in our vocabulary. Each edge $(u, v)$ will be equal to $P(v ~|~ u)$ where $u$ and $v$ are words. Note that this graph goes on forever, and that we have a $\text{</s>}$ token for ending a sequence. Thus, finding out the most likely sequence of words is equivalent to finding the longest path in this graph.

(an illustration of how we "search" for the most probable sequence)

As we know, the longest path problem is famously NP-Hard, which means that trying to maximize

for an entire sequence is thereby also NP-Hard since they are equivalent problems. As a result, solving our little text decoding problem in polynomial time could net you one million dollars! People have tried to do this for a long time with little luck, so let's look into approximating this problem instead.

Approaches

There are a lot of ways to approximate the task of generating natural language. I really like the paper The Curious Case of Neural Text DeGeneration, which introduces Top-P Sampling and reflects on previous approaches.

Greedy Decoding

Our first and most intuitive approximation is known as Greedy Decoding, where we take the most probable word over a vocabulary $V$ for a context $c$ as the next word.

Repeatedly taking the most performing this operation will allow us to create a sentence, one word at a time. Unfortunately, this approach doesn't produce very convincing results, and tends to exploit weird patterns, even repeating itself due to cyclic dependencies (i.e. going back and forth between words that predict each other like "I went to the place that the place that the place that the place ..."). This approach also creates deterministic answers for a given start token, which definitely is not how humans approach language generation.

We can do better!

Beam Search

As with most naive approaches, Greedy Decoding doesn't always produce the best outcomes. This is especially true in certain domains such as translating between different languages, where tokens at the beginning of the sentence may dramatically alter the likehood of its following tokens. This creates the problem of a high-probability token "hiding behind" a low-probability token that preceeds it in the order of the sentence. As a result, Greedy Decoding will forgo the low-probabilty token in favour of another one, regardless of that token's subsequently generated tokens.

One approach that mitigates this problem is Beam Search, which is another greedy algorithm that approximates the search process by maintaining multiple possible candidates for a path (which each represent a sentence). This "beam" of results is ultimately a search heuristic that allows us to deterministically approximate the most likely sequence of words.

Beam Search works really well in translation settings, since there is often not too much creativity involved with translating sentences between languages, and it works extremely well for the task. However, for tasks such as dialogue and story generation, Beam Search is rarely used, since it can create boring text.

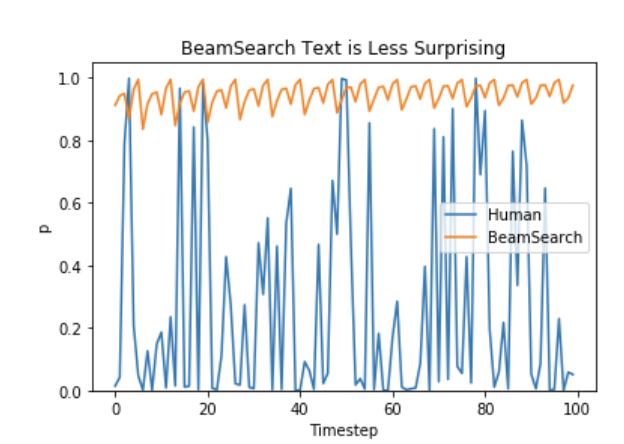(from Holtzman et al.)

As it turns out, there are more direct (and elegant) ways to approach this search tasks non-deterministically.

Random Sampling

The last way that we can generate text is to let uncertainy do it's thing and randomly sample directly from the distribution of $P(w ~|~ c)$. This might also feels like a naive way to do text generation, but in reality this allows for a good middle-ground between creativity and greediness. In expectation, the strategy tends to produce statistically likely sequences. For machine learning in general, relying on expectation tends to do well for us!

However, one issue with Random Sampling (and decoding strategies in general) is the lack of control we have over how the signal is used to select candidate words. Fear not, because we have ways of tuning the way our model uses the token probabilities to generate text. One main way to impose behaviour on decoding strategies by altering the output distribution of $P(w ~|~ c)$.

Top-K Sampling

The first way we can alter the probability distribution of the next word is to truncate the vocabulary to a certain length of the $k$ most likely tokens, and redistributing the truncated probability mass to these selected tokens. This has the effect of constraining the generation process to select words that the model itself has deemed to be more sensible in the context. This tends to produce more creative and human-sounding text!

However there's a tradeoff in the hyperparameter $k$. If $k$ is too large, then we basically have no benefit over vanilla random sampling. Conversely, when $k$ is too small, we have a limited vocabulary and the generated text will make even less sense.

A nice implementation tidbit about Top-K Sampling is that it's equal to vanilla random sampling when $k = |V|$, so the results of using a specific value of $k$ can be quickly evaluated against a distributional baseline.

Top-P Sampling

Top-P Sampling (or Nucleus Sampling) was introduced by Holtzman et al. in an aptly named paper: The Curious Case of Text Degeneration. In this sampling method, instead of predefining the $k$ most likely tokens, we instead only consider the words which have a cumulative probability mass larger than the hyperparameter $p$.

Intuitively, this is a natural extension of Top-K Sampling, since we're trying to mitigate the effects of the "unreliable" tail end of the distribution over the next word. The main difference is that we rely on a probabalistic approach (which can be more robust) instead of a function of the vocaulary size.

Temperature

Yet another hyperparameter we can use to alter the probability distribution of the next word (specifically when generating text with neural networks) is known as temperature $T$. Intuitively, this controls how "confident" the model must be before making a prediction about the next word.

When temperature is high (e.g. $T = 1$), the model can rely on its original predictions, without worrying about how confident it has to be. This has the effect of the network being more creative and diverse, at the risk of making more language errors.

However, lowering the value of $T$ closer to zero makes the output distribution more "soft", meaning that the neural network has to be more confident in its predictions. As a result, the network's most confident prediction will trump the probability of the others, resulting in less diverse, but more coherent text.

Conclusion

So it seems like there are a lot of decoding strategies for generating text. For deciding which to use, it's best to think about what aspect of human language you are trying to capture. If it's an accuracy-maximizing translation task, then Beam Search is the way to go (determinism in selection can be helpful). If you want the expressiveness and character of a chatbot, then random sampling with a distributional change would make the most sense.

Another interesting note is that I've largely tried to abstract how we get the distribution $P(w ~|~ c)$. In modern times, we use neural networks to do this (the current state of the art at the time of writing this post are Transformer networks), but the logic from this blog posts applies even if you do a simpler Markov Chain to yield the distribution of the next word.

Trying to use statistical and mathematical tools to decipher what makes text sound human is an interesting avenue of research and lately I've been exploring it in earnest. Check out this project here to see our latest efforts!

References

1. Theory: (Ippolito et al.)
2. Code: (HuggingFace)